Как реализовать алгоритм бинарного поиска на Python

Двоичный поиск — известный алгоритм в компьютерной науке, который можно реализовать на многих языках, включая Python.

Это алгоритм, позволяющий находить элементы в отсортированном массиве. Его часто упоминают на соревнованиях по программированию и технических собеседованиях.

Вы всегда должны использовать существующие библиотеки при выполнении бинарного поиска в Python или любом другом языке. Мы делаем исключение в этом руководстве, чтобы вы могли понять, как работает бинарный поиск.

Для прохождения этого урока вам необходимо иметь базовые знания о конструкциях Python и типах данных, таких как кортежи, списки и словари.

Начнем!

Что такое бинарный поиск?

Алгоритм бинарного поиска позволяет находить элементы в отсортированном массиве. Он более эффективен, чем другие алгоритмы, такие как линейный поиск.

Например, предположим, что у вас есть массив из десяти тысяч элементов, и вы хотите найти индекс определенного элемента в массиве.

Двоичный поиск обеспечивает очень быстрый способ нахождения индекса элемента, который вы хотите найти.

Давайте рассмотрим шаги по реализации бинарного поиска.

• Первым шагом является сортировка массива. Сортировка означает расположение элементов массива в определенном порядке.
• Разделите массив на две половины, определив индекс среднего элемента в массиве.
• Сравните средний элемент со значением, которое вы хотите найти. Если элемент совпадает, то верните индекс этого элемента.
• Если значение, которое вы хотите найти, больше среднего элемента, то возьмите вторую половину массива и снова разделите ее на две половины.
• Если значение, которое вы хотите найти, меньше среднего элемента, то возьмите первую половину массива и разделите ее на две половины.
• Процесс продолжается до тех пор, пока средний элемент не совпадет со значением, которое вы хотите найти.

Для начала давайте разберемся, что означает сортировка, посмотрев на картинки ниже:

На рисунке выше у нас есть несортированный массив целых чисел. Первым шагом к реализации алгоритма бинарного поиска является его сортировка.

В наших примерах кода мы сохраним этот массив в списке Python:

numbers = [31, 2, 12, 75, 3, 34, 6]

После сортировки списка мы определим две переменные: low и high.

Переменная low представляет индекс 0 в списке. Переменная high представляет последний индекс в списке.

В нашем случае значение low равно 0, а значение high равно 6 (индекс последнего элемента).

Теперь давайте вычислим средний индекс списка, используя следующую формулу:

mid = low+(high - low) // 2

Рассчитайте средний индекс с помощью оболочки Python:

>>> low = 0
>>> high = 6
>>> mid = low+(high - low) // 2
>>> mid
3

Таким образом, середина будет иметь индекс 3, как показано ниже:

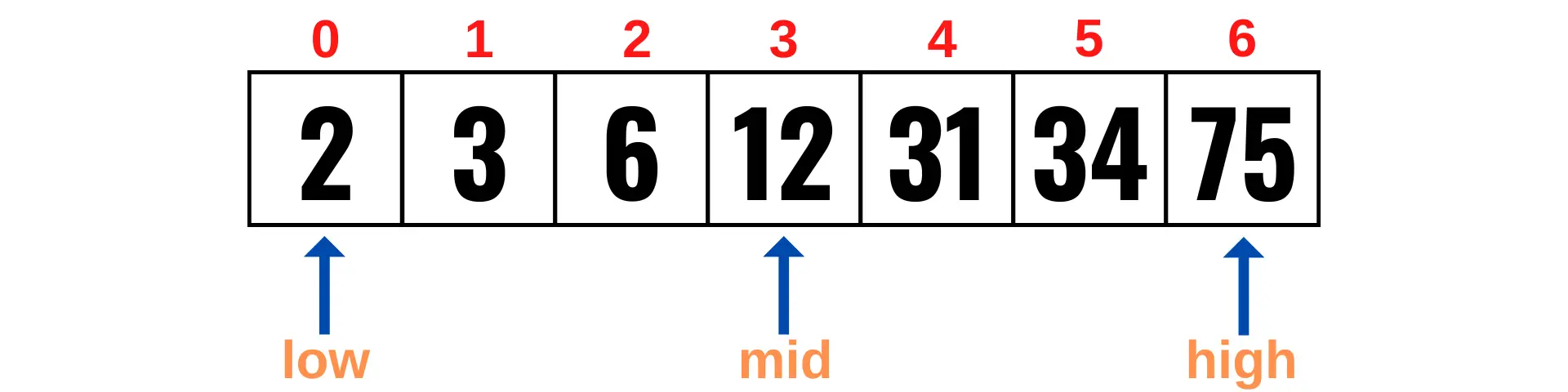
Теперь выберите элемент в этом списке и найдите его с помощью алгоритма бинарного поиска. Давайте используем число 31.

Алгоритм бинарного поиска сначала сравнивает число 31 со средним элементом. Если они равны, бинарный поиск возвращает индекс среднего элемента.

if item_to_find == values[mid]:
           return mid

Если искомое число больше середины списка, то переменная low переместится на один элемент после середины, как показано ниже.

elif item_to_find > values[mid]:
            low = mid+1

На этом этапе мы делим массив на две половины и снова вычисляем правую половину массива (которая больше середины).

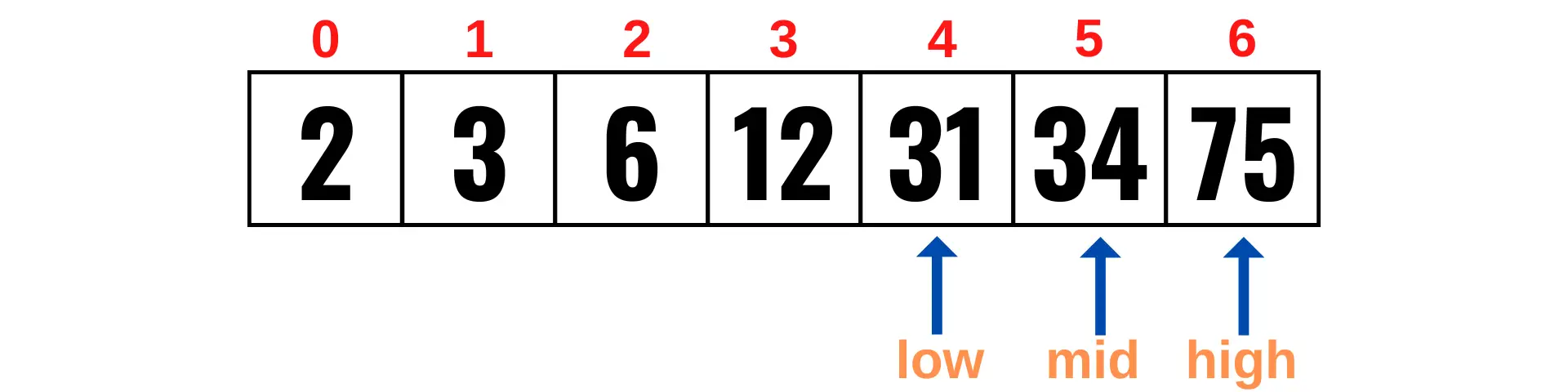
Число 31 не равно среднему значению (34), на самом деле оно ниже среднего значения, поэтому двоичный поиск устанавливает значение высокого значения на среднее значение – 1.

elif item_to_find < values[mid]:
            high = mid - 1

Вы можете видеть, что в этой точке low, high, и mid — это одно и то же число. Это число, которое мы ищем (31).

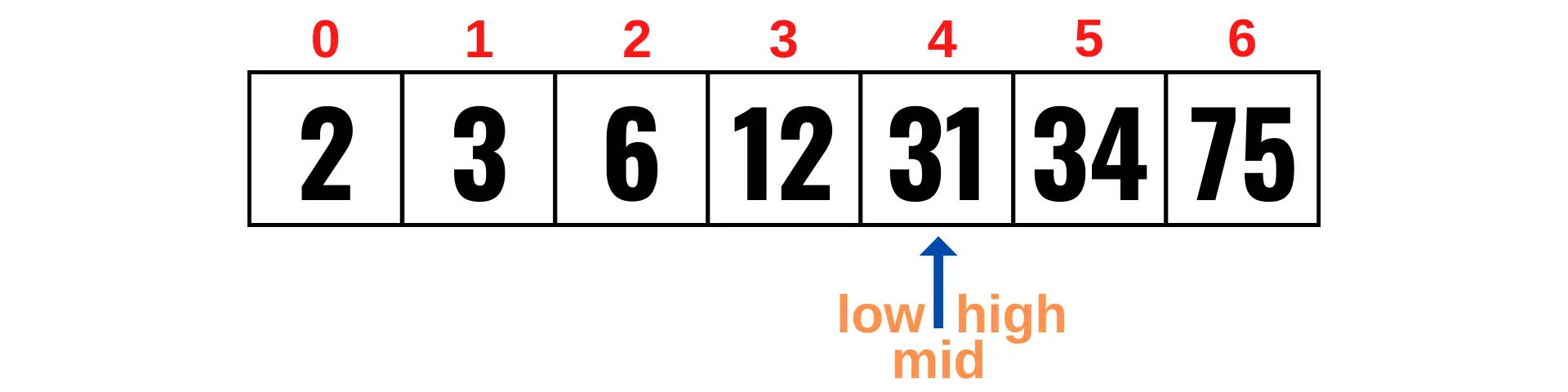
Алгоритм двоичного поиска называется двоичным, потому что он снова и снова делит список на две половины до тех пор, пока искомое значение не будет найдено (средний элемент).

В следующем разделе мы увидим, как реализовать алгоритм бинарного поиска с использованием Python.

Как реализовать алгоритм бинарного поиска на Python

Мы можем реализовать бинарный поиск двумя способами:

• итеративный бинарный поиск
• рекурсивный бинарный поиск

Мы рассмотрим, как реализовать оба варианта, и поработаем над отсортированным списком.

Начнем с реализации итеративного бинарного поиска на Python, основанного на цикле while.

def iterative_binary_search(low, high, values, item_to_find):
    while low <= high:
        mid = low+(high - low) // 2

        if item_to_find == values[mid]:
            return mid
        elif item_to_find < values[mid]:
            high = mid - 1
        elif item_to_find > values[mid]:
            low = mid+1

    return -1

Мы определили функцию iterative_binary_search(), которая принимает список и число, которое мы хотим найти, в качестве параметров. Мы также передаем самый низкий и самый высокий индексы в списке (low и high).

Цикл while выполняется до тех пор, пока значение low не станет меньше или равно значению high.

В теле цикла while мы сначала вычисляем индекс середины списка. Вы уже видели, как работает формула середины ранее в этом уроке.

После вычисления среднего индекса можно использовать оператор if для реализации следующей логики:

• Если искомое число равно среднему элементу списка, мы возвращаем средний индекс.
• Если искомое число меньше среднего элемента списка, мы делим список пополам и берем левую часть списка (устанавливая значение high равным mid – 1).
• Если искомое число больше среднего элемента списка, мы делим список пополам и берем правую часть списка (устанавливая значение low равным mid+1).

Этот процесс продолжается до тех пор, пока искомое число не совпадет с элементом, указанным средним индексом.

Теперь давайте проверим наш код и попробуем найти число 31 в нашем списке:

if __name__ == '__main__':
    numbers = [2, 3, 6, 12, 31, 34, 75]
    number_to_find = 31

    # Executing iterative binary search
    iterative_number_index = iterative_binary_search(0, len(numbers) - 1, numbers, number_to_find)

    if iterative_number_index!= -1:
        print(f"Iterative Binary Search: Number {number_to_find} found in the list at index {iterative_number_index}")
    else:
        print(f"Iterative Binary Search: Number {number_to_find} not found in the list")

Оператор if в первой строке полезен, когда вы импортируете функции из этого модуля Python и не хотите выполнять код внутри блока if.

При выполнении этого кода вы получите следующий результат:

Iterative Binary Search: Number 31 found in the list at index 4

Вывод правильный, поскольку индекс искомого нами значения в списке равен 4.

Что такое рекурсивный двоичный поиск?

Мы также можем использовать рекурсивный подход для поиска любого элемента в нашем списке Python с помощью бинарного поиска.

Рекурсия означает, что наша функция вызывает себя до тех пор, пока значение, которое мы хотим найти, не совпадет со значением, указанным индексом middle.

Подобно предыдущему подходу, этот продолжает разбивать список на небольшие части, пока не найдет элемент.

Вот рекурсивная реализация бинарного поиска:

def recursive_binary_search(low, high, values, item_to_find):
    if low <= high:
        mid = (low+high) // 2

        if item_to_find == values[mid]:
            return mid
        elif item_to_find < values[mid]:
            return recursive_binary_search(low, mid - 1, values, item_to_find)
        elif item_to_find > values[mid]:
            return recursive_binary_search(mid+1, high, values, item_to_find)
    else:
        return -1

Мы определили функцию recursive_binary_search(), которая принимает список и число, которое мы хотим найти, в качестве параметров. Мы также передаем самый низкий и самый высокий индексы в списке (low и high).

Функция вычисляет середину, затем:

• Если средний элемент равен искомому числу, функция возвращает индекс среднего элемента.
• Если искомое число меньше среднего элемента, то та же функция вызывается рекурсивно, сохраняя то же значение для low и обновляя high до mid – 1.
• Если искомое число больше среднего элемента, то та же функция вызывается рекурсивно, сохраняя то же значение для high и обновляя low до mid+1.

Обратите внимание, что обновленные минимальные и максимальные значения передаются в рекурсивный вызов функции.

Теперь проверим этот код:

if __name__ == '__main__':
    numbers = [2, 3, 6, 12, 31, 34, 75]
    number_to_find = 31

    # Executing recursive binary search
    recursive_number_index = recursive_binary_search(0, len(numbers) - 1, numbers, number_to_find)

    if recursive_number_index!= -1:
        print(f"Recursive Binary Search: Number {number_to_find} found in the list at index {recursive_number_index}")
    else:
        print(f"Recursive Binary Search: Number {number_to_find} not found in the list")

Давайте убедимся, что результат такой же, как и при итеративном подходе, который мы использовали в предыдущем разделе:

Recursive Binary Search: Number 31 found in the list at index 4

Результат правильный!

Какова временная сложность бинарного поиска?

Вот значение временной сложности для алгоритма бинарного поиска в лучшем, среднем и худшем случае:

• Лучший случай: это происходит, если искомое число является средним элементом отсортированного списка. Лучший случай сложности алгоритма бинарного поиска с использованием нотации Big-O является постоянным и представляется как O(1).
• Средний случай: средняя сложность алгоритма бинарного поиска с использованием нотации Big-O является логарифмической и представляется как O(logn).
• Худший случай: наихудшая сложность алгоритма бинарного поиска с использованием нотации Big-O является логарифмической и представляется как O(logn).

Как протестировать алгоритм бинарного поиска на Python

После создания наших функций бинарного поиска мы протестировали их с одним входным значением.

Но чтобы убедиться, что мы реализовали бинарный поиск правильно, нам нужно протестировать обе функции с каждым элементом в нашем списке.

Мы могли бы сделать это вручную, но есть способ получше…

…используя модуль Python unittest.

В том же каталоге, где вы создали модуль Python, содержащий обе функции бинарного поиска, создайте файл с именем test_binary_search.py.

Этот файл будет содержать код для тестирования обеих функций бинарного поиска с использованием модуля unittest.

Начнем с тестирования итеративной функции:

import unittest
from binary_search import iterative_binary_search

class TestBinarySearch(unittest.TestCase):

    numbers = [2, 3, 6, 12, 31, 34, 75]

    def test_iterative_binary_search_with_numeric_list(self):
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 2), 0)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 3), 1)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 6), 2)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 12), 3)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 31), 4)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 34), 5)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 75), 6)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 76), -1)

if __name__ == '__main__':
    unittest.main()

Мы определили класс TestBinarySearch , который наследует unittest.TestCase.

Затем мы использовали несколько утверждений в методе test_iterative_binary_search_with_numeric_list(), чтобы протестировать этот алгоритм на каждом элементе нашего списка.

Давайте выполним этот код:

(python-env) # python test_binary_search_iterative.py 
.
----------------------------------------------------------------------
Ran 1 test in 0.000s

OK

Тест пройден успешно!

Теперь добавьте утверждения для проверки рекурсивной реализации алгоритма бинарного поиска:

import unittest
from binary_search import iterative_binary_search, recursive_binary_search

class TestBinarySearch(unittest.TestCase):

    numbers = [2, 3, 6, 12, 31, 34, 75]

    def test_iterative_binary_search_with_numeric_list(self):
        [This method doesn't change...]

    def test_recursive_binary_search_with_numeric_list(self):
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 2), 0)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 3), 1)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 6), 2)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 12), 3)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 31), 4)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 34), 5)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 75), 6)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 76), -1)

if __name__ == '__main__':
    unittest.main()

Выполните оба теста:

(python-env) # python test_binary_search_iterative.py
..
----------------------------------------------------------------------
Ran 2 tests in 0.000s

OK

Оба теста прошли успешно!

Заключение

Алгоритм бинарного поиска отлично подходит для поиска элементов в отсортированных списках Python. Причина, по которой этот алгоритм быстр, заключается в том, что он избегает ненужных сравнений.

Вы реализовали простые примеры на Python, которых должно быть достаточно, чтобы понять, как работает этот алгоритм поиска. Мы рассмотрели два подхода к бинарному поиску: итеративный и рекурсивный.

И наконец, вы узнали, как протестировать наши две функции бинарного поиска с помощью модуля Python unittest, а также как временная сложность применяется к алгоритму бинарного поиска.